- Home
- Nekoreguojami
- Search
Search
2023. 07. 18
-
When a surname becomes a scientific term: chaos control by Prof. K. Pyragas
If you enter the keyword "Pyragas" in the social network Research Gate, the system will offer you a large number of articles by scientists from all over the world mentioning this name.
"Equivariant Pyragas control of discrete waves", "Quantum Pyragas control", "Current Oscillator Based on Pyragas Model", "Stabilization of Hyperbolic Chaos by the Pyragas Method"... Complex terms and research inspired by the work started by a Lithuanian physicist.
"I don't even know... I don't keep track of who is doing what anymore," says Professor Kęstutis Pyragas, Chief Scientist of the Department of Fundamental Research at the Center for Physical Sciences and Technology (FTMC), when asked if he has counted the number of similar papers.
"But there is one I am particularly proud of. It is the 2022 article: it has both Pyragas' and the famous Schrödinger's name in one title. And now my method has been applied to quantum mechanics", laughs the physicist.
In 1992, after writing a less than 8-page article in the prestigious journal Physic Letters A on his proposed mathematical method for chaos control, he eventually became the most quoted Lithuanian scientist of all time. According to Google Scholar, he has been cited approximately 4,500 times.
Pyragas' chaos control method is used in a wide range of experiments and research, from physics, chemistry and medicine to economics, robotics and electronics.
On 16 February 2023, President Gitanas Nausėda awarded Professor Pyragas the Officer's Cross of the Order of the Grand Duke Gediminas "for his significant contribution to the development of physical science, his world-class discoveries which has earned him a name inseparable from the most significant achievements in physical science".
Physics is very much a part of the Professor's life: his wife, Dr. Tatjana Pyragienė, works in the same department at FTMC, as well as his son Viktoras. His daughter Viktorija has chosen a slightly different field of physics - laser technology.
It is with the family of Prof. Kęstutis Pyragas that we begin our conversation. His scientific career is impressive, but his personal story is no less strong.

(The whole Pyragas family in Siberia. The youngest child Kęstutis is sitting at the bottom, second from the left. Aleksandrovskoye village, Tomsk Oblast, Russia, 1956. Photo from personal archive)
It is very interesting to hear about the very beginning. What is your family history? As far as I have been able to find out, you were born in exile, but this has never been written about in any detail.
A very large family was exiled from Lithuania. My mother and father raised twelve children - ten brothers and two sisters. When I was deported, my mother was expecting me, and I was born in Siberia, the youngest child.
Two of the children, the eldest sons, were arrested as partisans before that, and they were sentenced to ten years in prison, but they were released after Stalin's death.
What were you all deported for?
There was nothing to accuse them of. They were taken to Siberia as a standard practice, because there they had to work the land. And not only for that. They took all the intelligentsia, wealthy farmers. They were destroying the whole essence of Lithuania.
There were so-called troikas, where three people had to sign an 'accusation'. The Soviets had to have some documents processed before the deportation, and there was a quasi-thesis. It was usually signed by three neighbours, some drunkards who knew: when they were deported, I could take my bed out of their house, or something like that... There was always one or two of them in the village who supposedly testified. Three were enough for the whole village (laughs).
My parents and their family were in hiding for a very long time. People would find out that a train was coming and they would tell others that there would be a new deportation. Then, in those days, people would go into hiding: the whole family would run away, they wouldn't go home. And if they are not caught that time, they return home a few days later. Until the next danger.
On the fateful day when we were taken away, there was a potato harvesting. The family was digging potatoes, everyone was tired. Even though they were informed of the danger, they did not go into hiding, but stayed at home to sleep. And they were arrested...
How many years did you have to stay in Siberia?
Until 1957, four years after Stalin's death.

(Kęstutis (right) with his older brother Pranas. Aleksandrovskoye village, Tomsk Oblast, Russia, 1957. Photo from personal archive)
You were five at the time, and you probably don't remember much of that period yourself. But what have your family members told you about it? It's hard to imagine what a family with so many children must have gone through in Siberia...
I'm sure so. What a stress for the parents - they are taken away, they are not allowed to take anything with them. But they managed to survive. Even more: before leaving Siberia, the family managed to build a second house! People told them: "You need to be deported somewhere else, because you've turned into kulaks!" (laughs)
So your parents were hardworking and not giving up?
And the children were already grown up. The first two were in the labor camps, and the others, the older ones who stayed with the family, were already 18 or 20 years old.
What is even more interesting is that everyone there was forced to work in a kolkhoz. If you agree with that, they take away your passport, you become stateless and you can't go anywhere. Soviets tried to force my father and my older brothers, but they didn't sign anything, they stood firm. And that saved us, because later we could leave.
How did it go when you returned to Lithuania?
The story is extraordinary. At first we came back to Lithuania, but everything had already been destroyed and our house was gone. We stayed for a short time with relatives. Two of my brothers were looking for work in the Soviet Union until they found a place in Kazakhstan, working as construction workers in a mining town.
At that time there was a need for a work there, and they gave you an apartment right away. And then my brothers invited our family to Kazakhstan. It was a second exile, but it was "voluntary".
I started school there, finished five grades. The other brothers went to higher education, but in other republics of the USSR. Except for me, most of them worked and graduated from evening schools; my parents allowed me to be the only one to finish full-time school. Despite having to work, almost everyone managed to get a higher education.
Five brothers got physics degrees. Overall, out of ten brothers, only two did not finish high school. Neither did the girls, by the way, apparently because there was always hard work to do at home. Still other brothers had a degree in construction - they didn't want to go into the mines because it was too dangerous, but they built houses for the miners.
What made so many children in your family graduate from higher education? Parental influence?
My father was a village teacher. As far as I know, he taught my mother at school (laughs). In the old Lithuanian countryside, education was held in very high esteem, and parents were keen to see their children get an education. Already in Siberia, my parents wanted their children to pursue education, they understood the need for it.

(Liepkalnis School in Vilnius (formerly 28th Secondary School), where Kęstutis Pyragas studied. Photo: Prancuze / Wikipedia.org)
You yourself completed five grades in Kazakhstan, and then?
At that time, my brother and I were the last two to stay with my parents, and everyone else got married, went to university and left. The rest of the family - the four of us - came back to Lithuania in 1964 and stayed with my sister who had built a house. Then the older brothers scraped together some money and bought a cooperative flat for my parents in Antakalnis, Vilnius.
Later, my older brother went to study at Kazan State University, where my other two brothers were already studying. And I finished school in Vilnius.
Which one?
I graduated from a Russian school, by the way. It was then the 28th Secondary School in Vilnius [now Vilnius Liepkalnis Elementary School - S.B.]. My parents propably have made a mistake about that (smiles). I spoke Lithuanian, but I wrote badly. And then I entered Vilnius University, also in the Russian group.
You chose to study physics. Four brothers influenced you?
It's hard to say now. But I think the brothers' examples were crucial. Although I had very little contact with them. They left quickly, and I only knew that they were studying physics.
I had a very good physics teacher at school, Povilas Repšas, and I was also interested in physics myself.
What attracted you to physics?
I don't know, I really liked it. I liked solving physics problems at school. My teacher noticed that and started working with me individually. I come to class, but I don't listen to it - the teacher gives me the exercises individually and we discuss them at the end of the class.
When I left school, I went to the Moscow Institute of Physics and Technology, the best in the Soviet Union. I took exams and solved exercises in the Olympiads, but I was not properly prepared and did not pass the competition.
Perhaps last but not least, I was an exile. I think that may have played a role, too.
I was just about to ask, what was it like in Soviet Lithuania? Did the fact that you were born in exile interfere?
Of course. For my brothers, it did, Soviets didn't want to register them in Lithuania at first. And those who were in the labor camp were not registered at all.
What about academic activities? Did you feel that you were being picked on, that your career was being hindered?
When I was studying at university, there was a military department. I really felt it there, very strongly. I was the only Lithuanian in that Russian group. There was Colonel Safronov, the head of the military department. He gnashed his teeth at me. When I had to serve in the army for two months after graduating from university, he made fun of me on purpose. Because I was born in Siberia.
How did you react to such things?
Obviously, unpleasantly (smiles). But I understood everything.
Then I saw that Safronov after Lithuania had already declared its independence from the Soviet Union. There was an economic reform by the then Prime Minister Kazimiera Prunskienė, there was a very sharp increase in prices, and the Yedinstvo gathered in front of the Parliament. I was there too, and I saw that Safronov was one of their leaders. He was shouting that hot water was being poured on them from Parliament. Then I wanted to do something to him (laughs).

(Theoretical physicists in year 4. Kęstutis Pyragas is fifth from the left, with his future wife Tatjana in the middle. Vilnius, 1973. Photo from personal archive)
You were a student and then you taught at the university. What would you say is so striking about that period?
I had a quiet time during my studies. But then I was very lucky with an appointment - when I was doing my coursework in the 4th year, I came to the then Semiconductor Physics Institute and got a supervisor, Prof. Algirdas Matulis. He was a real physicist, he always wanted to get to the point. He was doing real science: you could feel it when you were with him.
I started out interested in semiconductor physics only and did my PhD. Back in the Soviet times, at a scientific conference (then in Gorky, now Nizhny Novgorod), I heard about chaos for the first time in my life - that was the very beginning of this science.
I started to apply it to semiconductors, and then I went into the science of chaos theory.
Perhaps it is time to talk about it. Could you explain in simple words what chaos is in physics?
Probably most people understand it as disorder.
My children's room comes immediately to mind...
There you go. Or this table that we're sitting at - look, things are scattered around, and so on.
There would be chaos in the space. And the chaos I'm interested in is chaos in time. When something in time changes in a very disorderly way.

(Prof. Kęstutis Pyragas. Photo: Domas Jokubauskis / FTMC)
I once heard an example from you - if you drop a ball into a bowl, we don't know how it will bounce.
Not in a bowl, but in a different way. Let's say a plane that moves up and down in a nice periodic way, and we let a ball bounce on it. It will bounce in a very disorderly way. The plane will move in an orderly way, but the ball will not.
As another easy example, the price movement of a bitcoin, euro, dollar or other currency is also random, chaotic. There is nothing regular.
Such fluctuations need to be analysed in mathematical terms as to how they can arise. To do this, we need to understand the dynamical system and other things.
One of the scientific approaches is that everything is determined: if I know that a particle is moving at a certain speed and in a certain place, and if it is subject to a certain known force, I can calculate unambiguously what will happen in a minute, or two minutes, or three dozen minutes. Knowing the initial conditions of the system, I can predict into the future the entire evolution of the system.
This is called Laplace determinism. This French mathematician said: if you gave me the initial conditions of all the particles in the Universe, I could tell you what will happen to the Universe in millions of years, and so on. This is the optimistic view (smiles).
But...
But it's really not. One of the reasons is that determinism exists only in the macroworld.
You mean stars and planets?
Not only that, but what we see around us here in the office, all the things around us - that's also the macroworld.
The microworld is therefore molecules and atoms. So, at the microscopic, atomic level, determinism no longer exists. There, it is no longer Newton's laws that are at work, but the Schrödinger equation, which describes random processes. From the initial conditions, the future cannot be predicted unambiguously - only probability.

(Photo: Pexels.com)
Is this where quantum physics comes in?
Yes.
But chaos theory, not only at the micro level, but also at the macro level, has disproved that it is possible to predict the future. If you want to do that, i.e. to describe everything deterministically, you need to determine the initial conditions as precisely as possible. These are determined experimentally. Any experimental measurement has a margin of error. In systems with chaotic behaviour, this error grows very rapidly, exponentially, over time.
I can illustrate the exponential growth with the example of a chessboard. There is a legend: the man who invented chess several thousand years ago showed it to his king. He liked chess, and he said: "I can pay you whatever you want for it." The man replied: "I want very little: on the first square of the chessboard you will place a grain for me. On the second, you will give two grains. Four grains on the third. And so on, doubling and doubling."
The lord found the offer very silly and agreed. His mathematicians spent the whole night calculating how many grains would be needed, and when they reached the 64th square, they realised that there were no more grains on Earth (smiles).
The exponential law of growth is so fast that it is beyond the mind's comprehension.
Another example. Imagine that if you put money in the bank, it would double every year. If you put in one euro, you would be a millionaire in 20 years.
So, the error in time grows very fast. Let's say we have an accurate model and we want to use it to predict a real natural phenomenon. That model needs initial conditions, which are experimentally determined with an error. A tiny error will cause the solution of the exact model to diverge exponentially fast from the real experiment - so that after a certain time, called Lyapunov time, the whole prediction will be corrupted, worthless. And this is already true for Newton's laws, for the macroworld.
As far as chaos theory is concerned, mathematical concepts such as linearity and non-linearity are also needed.
What are these?
Imagine: if a car travels at a constant speed, the distance travelled increases linearly with time.
.jpg)
(Photo: Unsplash.com)
I drive at 100 km/h, and if that speed remains constant, I will have driven 100 km in an hour, 200 km in two hours, and so on?
Yes. This is linear growth.
But if I accelerate, if I press the accelerator occasionally, then the increase will be non-linear, the curve I've drawn will change. The distance will no longer grow linearly, but according to a new law.
The general mathematical apparatus that describes these laws of prediction says: if I want to describe a prediction, I need to know the laws of dynamics. And these are described by differential equations. That is the concept that is needed, and you cannot get away from it (smiles).
Differential equations relate the velocities of the variables (how much the variables in the system will change in a very short period of time) to the values of the variables themselves. The velocities are functions of those variables. Given the initial values of the variables, such equations can be used to determine the complete evolution of the variables over time. This is the mathematical definition of a dynamical system.
If the differential equations are expressed as linear functions, then they are very easy to solve and analyse, the answer is always known and there is no chaos. But if the equations contain non-linear laws, then we can no longer find a formula for how things are changing: they can only be solved by computer.
For a long time, it was unknown how nonlinear differential equations could "behave" because there were no computers. But the French mathematician Henri Poincaré made a major breakthrough in the 19th century: he qualitatively investigated all the possible solutions to two coupled differential equations. The solutions of such equations can be represented by the trajectories of a point moving in a plane. This geometrical interpretation led to the conclusion that the solutions of two differential equations eventually settle down either into constant, time-independent quantities or into strictly recurring periodic oscillations.
This was the long-held view that only two types of state can settle in dynamical systems: either a stationary, time-independent state or a state of strictly periodic oscillations.
Which is like waves?
Yes. And when scientists started using computers to solve larger systems, it turned out that just three variables of differential equations were enough to give chaotic solutions. They may not vary in time periodically, but in a completely chaotic way.
The so-called butterfly effect, where the solutions become sensitive to very small changes in the initial conditions, is a good description of this phenomenon.
.jpg)
(Photo: Unsplash.com)
The butterfly effect is a much heard term.
Edward Norton Lorenz, an American meteorologist, looked at the simplest weather forecasting models, which he brought together in 1963 into three simple differential equations, now called the Lorenz equations, and analysed them on a computer. When he realised the remarkable dependence on initial conditions, he called it the butterfly effect.
Lorenz says: let's say we know exactly the equations that describe the weather, and we have even measured the initial conditions - pressure, temperature, etc. - with perfect precision, and then a butterfly flies by, and the flap of its wings just barely changes the pressure. That's enough to cause the weather forecast to collapse a week later.
Interestingly, Poincaré's remarkable sensitivity to initial conditions was also discovered in the 19th century when he was working on the three-body problem, which he solved using approximate mathematical methods rather than a computer. Unfortunately, Poincaré's research was not properly appreciated by the scientists of his time and was forgotten. The butterfly effect only became generally accepted after Lorenz's work.
Can a simple butterfly really have such an effect on a system?
Yes, indeed it does. A very small change immediately changes the solution in a short time. Therefore, the time when a weather forecast will be reliable is about a week. This is a typical Lyapunov time for the Earth's weather system.
Is it impossible to forecast for a longer period of time?
No. It is a matter of principle.

(Prof. Kęstutis Pyragas. Photo: Domas Jokubauskis / FTMC)
And here we can already talk about the famous Pyragas' Chaos Control Method, which you first described back in 1992.
First of all, I can tell you how I came to it. It happened during our first trips to the West. It was maybe 1991 when I attended a big Western conference, I don't remember exactly where. And there I heard the first presentation on chaos control, because in 1991 three American scientists published a paper called 'Controlling Chaos', and one of them gave a presentation on it at the conference. I was very impressed by that, and when I came back I took up the subject.
And the idea is this. When you look at chaotic systems, in terms of mathematical models and differential equations, you can see a hidden order in them. If we run the differential equations from any random initial conditions, they will give a chaotic solution. However, it is possible to choose the initial conditions in such a way that the system gives a periodic rather than a chaotic solution.
What does this mean? All chaotic systems have so-called periodic orbits. There are lots of them, they look different - there are lots of periodic solutions, but they are all unstable, i.e. if you move away from an unstable periodic orbit for a little while, you don't go back to it.
The concepts of stability and instability can be explained with this simple example. Imagine a pit into which you throw a ball. It will fall to the bottom of the hole and if you move it, it will fall back to the bottom after a while. This is a stable state.
And the unstable state is when you put the marble on the very top of the mountain. It can stay there for a long time - you just have to be very precise. But if you move it just a little bit, it will roll down the hill and it won't come back.
In this sense, these are unstable periodic orbits in chaos. It exists in theory, but you can't see it in reality - because it's always "going downhill".
How to see it?
That state needs to be stabilised. And that can be done with feedback.
To bring that orbit-ball back to the "top of the mountain"?
Yes. If you observe this ball and see that it is starting to move one way or the other, give it a little nudge to get it back. And in this way, with a little force, watching its small movements, you can keep it on the top.
Chaos theory has a similar idea. It turns out that with a very small force it is possible to eliminate chaos and bring the system back to a periodic solution.

(Photo: Unsplash.com)
Is this applicable in practice?
My method has been experimentally implemented in systems of all kinds: mechanical oscillators, electronic chaos generators, lasers, chemical reactions, gas discharge, plasmas, ferromagnetic resonance, DC-DC converters, synchrotron terahertz frequency oscillators, fluid turbulence, atomic force microscopy, etc.
I won't go through everything here, but I will comment more on the last two realisations.
Turbulence in gases or liquids is often an undesirable phenomenon. Turbulence causes water eddies at the hull of a floating ship. They greatly increase friction. This limits the speed of the vessel and requires more fuel. Similar turbulence occurs at the wing of a flying aeroplane or the hull of a moving car. German scientists have shown in a real experiment that turbulence vortices can be successfully eliminated using my method.
Japanese scientists have successfully applied my method to stabilise an atomic force microscope. One of the ways in which such a microscope works is that, if I want to study a surface at the microscopic level, I have to make a very, very thin and pointed needle with a tip the size of an atom. This is now being done. And with that needle, I can scan the surface, to see how the atoms are arranged on it. The needle is vibrated by an external periodic field and it interacts with the molecular field of the surface. That interaction changes the phase of the oscillation of the needle and that gives information about the surface. The only problem was that the needle could start to move erratically when it interacted with the surface. And then the whole experiment fails. So the researchers, using my method, were able to bring back the 'normal', periodic oscillations of the needle.
The Pyragas Chaos Control Method involves time-delayed feedbacks. How can we understand this?
Simple feedback is similar to the control of the moving ball we mentioned. It is instantaneous feedback. As soon as the ball starts to roll off the top, it is immediately 'kicked' in the right direction. For the control of unstable periodic orbits, my method uses combined feedback, which consists of instantaneous and time-delayed feedback.
As far as time-delayed feedback is concerned, I will give two examples.
You take a shower. There are two knobs, one for hot and one for cold water. You want to choose the right water temperature. You have probably noticed that at first the water is either too cold or too hot (smiles). This is because from the moment you turn the knob, it takes a certain amount of time for the water to come through the shower hose at the desired temperature. That would be the feedback on the delay.
And there is also instability, because you have to turn the knobs before you get to the desired temperature, because the water will be too hot or too cold.
Another example. You teach a child to ride a bicycle and you tell him: when you feel yourself starting to fall, turn the handlebars in the same direction where the bicycle wobbles. The child understands this and does everything right, but he does it late. And we see that at first he rides with a wobble, before finally reducing the delay and then riding well. This is also an example of how delay brings instability.
According to the classical control theory developed by mathematicians, it was previously thought that delay always leads to instability. It was therefore "fought".
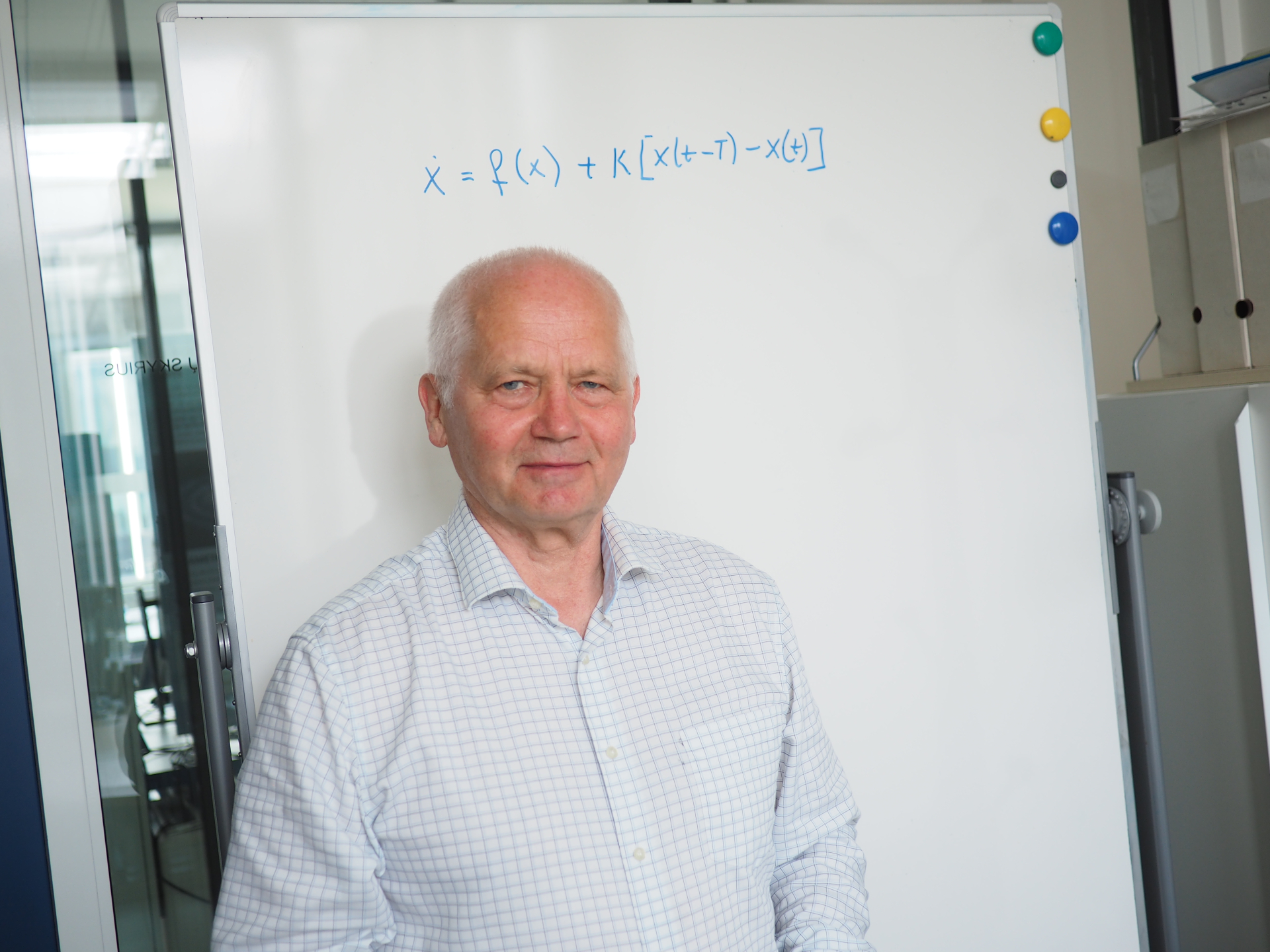
(Prof. Kęstutis Pyragas. Photo: Domas Jokubauskis / FTMC)
My chaos control method uses instant feedback alongside time-delayed feedback, so there is no instability. The beauty of the method is that it is written in a very simple formula.
Suppose we have a chaotic system which we imagine as a "black box", i.e. we do not have a model of the system, we do not know the equations that can describe the dynamics of the system. However, at the output of the system we can measure a time-dependent signal x(t). We also assume that the system has an input through which we can control it. If we apply a signal proportional to the output signal x(t), i.e. kx(t), where k is the coefficient of proportionality, to the input of the system, then we will realise the instantaneous feedback mentioned above. The coefficient k is also called the feedback strength. If we were to input a signal proportional to the time-delayed output signal kx(t-T), where T is the delay or latency time, we would realise time-delayed feedback.
My chaos control method uses the difference between the two signals. The signal fed to the system input is given by the one simple formula: k[x(t-T)-x(t)]. That's the whole point of the Pyragas method (smiles).
If I choose a delay T equal to the period of the unstable periodic orbit, then if the system moves in an unstable periodic orbit, the feedback force turns to zero, because of the definition of periodicity: x(t)=x(t-T). The control is disconnected when the system moves in the desired periodic orbit. However, if the system moves away from the desired periodic orbit, the feedback returns the system to the periodic orbit. Here, the feedback performs "kicks" similar to those that return the "ball" to the top of the mountain.
The system I am looking at is a black box, I do not know its equations. But I only need to guess the period of T. I can alternate it empirically and find it. Like k which is the strength of the feedback. I can find those two parameters empirically.
Although my chaos control algorithm is written down in a very simple formula and is easy to implement experimentally, its mathematical theory is complex. This is because the dynamical system so controlled is described by differential equations with delay, which are very complex. The complexity of the theory is a kind of success. I have not been alone in developing the theory of this method, and many theoreticians from all over the world have contributed to it.
You are now involved in neuroscience. What are you researching in particular? And how are time-delayed feedbacks useful here?
I met a German scientist, Peter Tass, who has two PhDs in medicine and physics. He is mainly involved in the treatment of Parkinson's disease.
The brain is made up of about a hundred billion neurons. Each of them is connected to tens of thousands of "neighbouring" neurons. A very complex system.
The physics and dynamics of a single neuron are fairly well understood by science. But how a neural network, a system of these connected neurons, works, we have a vague idea. Although we do see neurons 'spiking' - doctors attaching devices to a person's head and seeing disorganised neuronal signals coming from different parts of the brain.
Electroencephalographic (EEG) measurements show the behaviour of large numbers of neurons. The signal from a single neuron is very weak and cannot be seen in EEG measurements. EEG signals are observed when a large group of neurons behave in a coordinated - synchronised - way. EEG specifically shows signals from synchronised neurons.
Synchronisation is a very important brain function. Our thinking, our recognition of objects - everything is linked to synchronisation, although exactly how it works is still very unclear.
However, too much synchronisation can sometimes be harmful. Parkinson's disease is associated with abnormal synchronisation in a particular neuronal area. This leads to shaky hands and other problems.
My work in this area started out as a search for a solution to eliminate excessive synchronisation with feedback. A widely used instrument for this is called Deep Brain Stimulation, where electrodes are implanted in a specific area of the brain.
Previously, doctors who knew where in the brain of Parkinson's patients the abnormal synchronisation was occurring would remove that part of the brain.
Just cut it out?
Yes. You don't know what to do, you take it out and that's it. By the way, the brain is an amazing system. If some part of the brain is injured, the healthy parts of the brain can take over the functions of the injured part. The person can go on living.
A breakthrough in this field was made in 1991. A French scientist, Alim Benabid, was once approached by an ordinary patient. Instead of removing part of the brain, the specialist decided to try a different approach: he inserted a pair of electrodes into the brain, stimulated it with 100 hertz frequencies and saw that the patient's hands suddenly stopped shaking. This effect was discovered and stimulators - Deep Brain Stimulation - were launched. Nowadays, the implantation of such stimulators is a standard procedure in the treatment of Parkinson's disease.
But it is not a perfect treatment. The stimulator damages the brain, and over time you have to increase the electrical voltage... My task is therefore to make stimulators with feedback in the neural systems.

(Prof. Kęstutis Pyragas. Photo: Domas Jokubauskis / FTMC)
Would the device then be less harmful to the brain?
Yes, because very small signals would be enough to cancel out that excess synchronisation.
My field is not only Parkinson's disease, but also the dynamics of the neural network itself, it's behaviour. It is a very complex system, modern computers are not enough to understand what is going on. So I am looking at how to reduce very complex models to simple ones. How to make two equations out of ten thousand equations. This is called dimensionality reduction of models.
And another area where I work is artificial intelligence. Because it is also about neural networks, artificial neurons. I am involved in the prediction of chaotic systems. If I know how a system has behaved in the past, I want to predict from the signal I have analysed how that system will behave in the future.
My son Viktoras and I have also written an article on forecasting and managing extreme events. Let's say you observe a chaotic signal: for a long time, the oscillations are low amplitude and suddenly high amplitude. It is very similar to earthquakes: you observe small ground oscillations and then suddenly there is a big one. These are extreme phenomena.
Is it still very difficult for scientists to predict when the next earthquake will occur?
Yes. That's why we are trying to use artificial neural networks, artificial intelligence, to predict events.
Written by Simonas Bendžius
Related news:
-e0e907f6bc07ca7c0e2959f75812501a.jpg)
2023. 03. 22
-
Lithuanian professor has published a book that is read worldwide
There are only a few monographs on silicon electrochemistry in the world and the last one was written 20 years ago.
a-1c4665da2983c54a69676278eaef7e7e-d9b7263a49e9145e9f349f1f029562d6.jpg)
-24c208e22ff11fb358ebecc92d4e84c2.png)